Holt Mathematics Lesson 6-1 Relating Decimals Fractions And Percents Answers
We encounter ideas related to fractions, decimals, ratios and percents on a daily basis. Confident and flexible understanding of these ideas are key to everyday estimation and mental calculation in contexts as diverse as shopping and budgeting, diluting mixtures, understanding scales on maps, interpreting probabilities and odds, and converting among metric units.
Not only is understanding these ideas essential to being numerate they are also foundational to more sophisticated mathematical ideas. If you understand fraction, decimals, ratios and percents you have the basis for understanding topics such as similarity, trigonometry, coordinate geometry, and fancy algebra
Fractions, Decimals, Ratios and Percentages Pre-Test
Pre-Test for Module 2: Fractions, Decimals, Ratios and Percentages
Click on the link below to take the Pre-Test for Module . The Pre-Test is optional but we recommend taking it to test your knowledge of Fractions, Decimals, Ratios and Percentages. There are only 5 questions and it will only take about 10 minutes to complete.
If you receive 80% or greater on the Pre-Test, you have a good knowledge of Fractions, Decimals, Ratios and Percentages and can move on to the next module or review the materials in module 2.
If you receive less than an 80%, work your way through the module and then take the quiz at the end to test your knowledge.
Module 2: Fractions, Decimals, Ratios and Percentages
Fractions are useful in many contexts. Fractions are commonly used in everyday life as well as in mathematics.
Understanding 1
Part/Whole Concept
We use fractions every day, quite often to describe parts of a whole (e.g.,half an hour, third quarters of the football game, one quarter of a cup of sugar).
The part/whole meaning of fractions, expressed as 
, (where b≠ 0) is used when a part is being compared to the whole. The numeral above the dividing line (also known as the vinculum) is referred to as the numerator and the numeral below the vinculum is known as the denominator.
The numerator of the fraction (
) is 3 and the denominator is 5.
The numerator represents the number of parts of the whole and the denominator represents the number of equal sized parts into which the whole is divided.
The part/whole meaning of fractions can be demonstrated in the following everyday examples:
Example 1
If $5.00 is shared between two people, and person A receives $3.00 and person B receives $2.00, person A's share is three fifths () of the whole ($5.00) and person B's share is two fifths (
) of the whole ($5.00).
Example 2
A class of sixty (60) students is comprised of thirty six (36) females and twenty four (24) males. We can see that thirty six out of sixty (
) students are females and twenty four out of sixty (
) are males are males. The two fractions can be read as thirty six sixtieths and twenty four sixtieths.
This part-whole concept can be represented in a diagram:
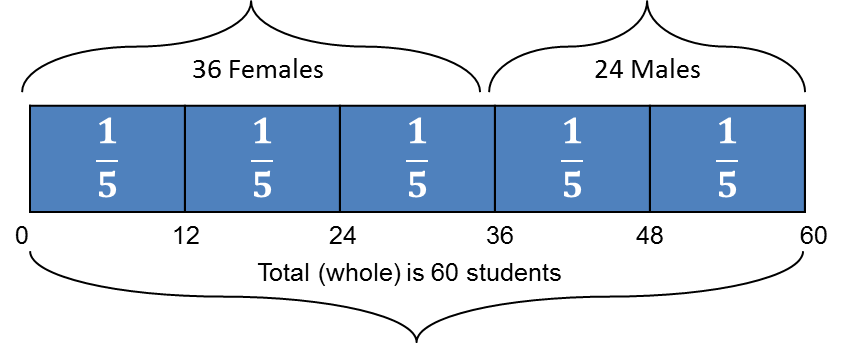
We see from the diagram that the "whole" (i.e., the total number of students) has been split into fifths (5 equal sized portions). Why fifths and not some other fraction? The reason lies in the fact that the highest number that can be divided exactly into 60 (the total number of students), 36 (the number of females) and 24 (the number of boys) is 12.
A common factor of both the numbers, thirty six (36) and twenty four (24) is twelve (12).
So: 60 ÷ 12 = 5 (therefore "the whole" has been divided up into 5 groups of 12. In other words, 12 is 
of 60).
Now, as 36 ÷ 12 = 3 the number of females represents(three fifths) of the total number of students.
Similarly, as 24 ÷ 12 = 2 the number of males represents(two fifths) of the total number of students.
Understanding 2
A Fraction is a number
A fraction is a number in its own right. For example, several fractions have been plotted on the number line below, just as we would plot any real number on a number line.
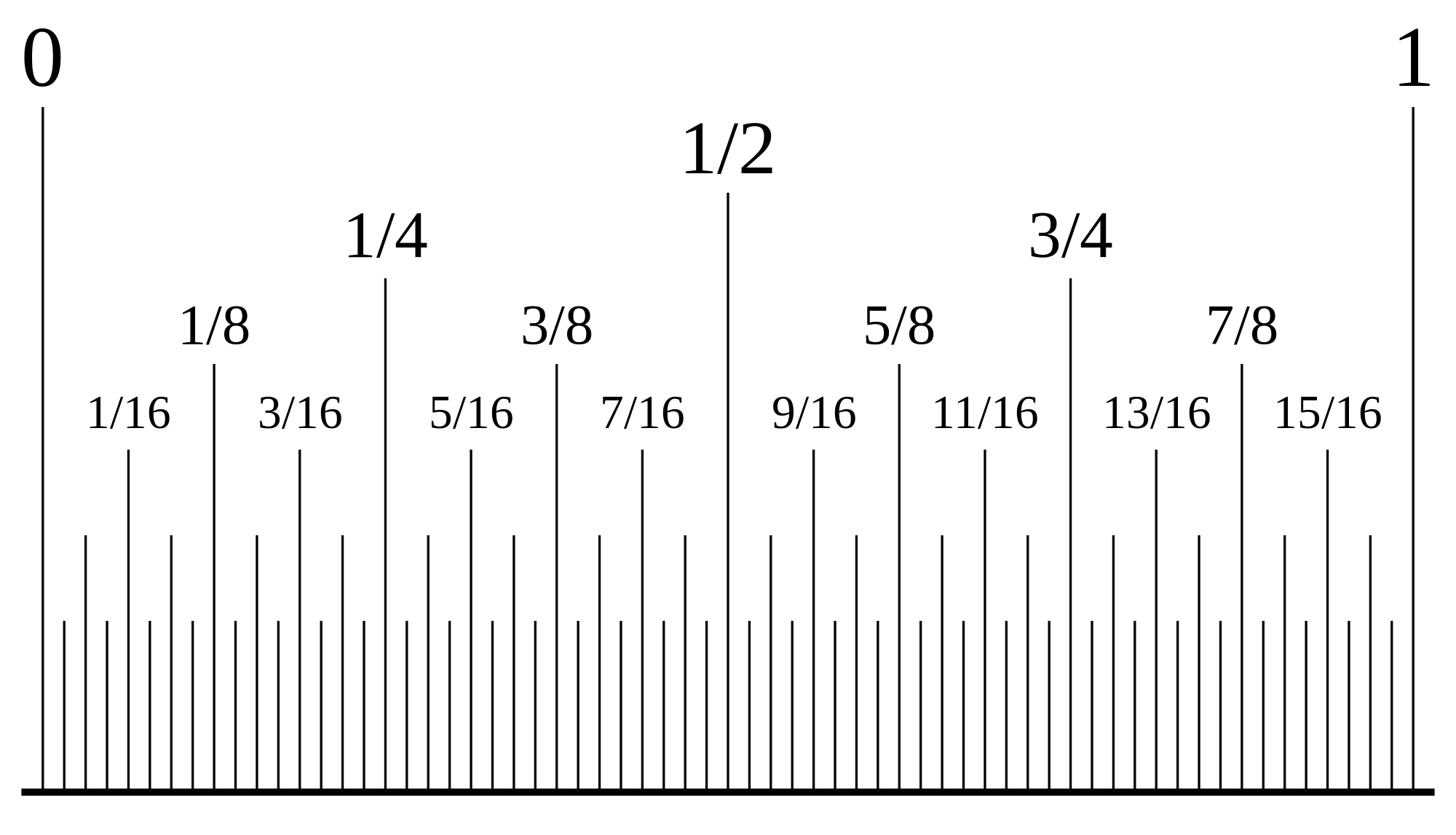Image: upload.wikimedia.org/wikipedia/commons/thumb/2/2f/Dyadic_rational.svg/2000px-Dyadic_rational.svg.png
The following video illustrates the notion of fractions as numbers by providing a brief overview of the development of fractions as part of the real number system. Before you watch the clip it may be useful for you to recall the meaning of the following terms "natural" number and "integer" by clicking on the following link Whole Numbers and Integers from Math Is Fun - Maths Resources.
The video also uses the "dot" symbol for multiplication (recall that a⋅b is equivalent toa ×b).
Understanding 3
Fractions on a Number Line
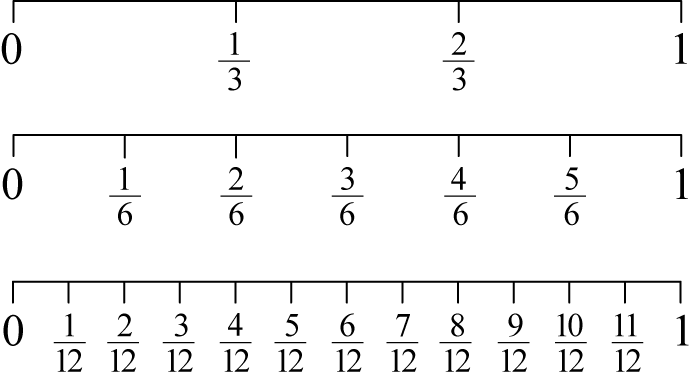
The number line below represents eighths, that is, fractions with a denominator of eight. Each one (whole) has been divided into eight equal parts.
To reach the three eighths position for example, three steps to the right are taken, starting at zero. Each step has a length of one eighth.
We can see that the fractions on the same point on the number line are equivalent fractions.
That is:
=
=
=
=
The following video demonstrates how to plot fractions on a number line, considering the number of total parts into the one whole needs to be divided (denominator) and the number of those parts to be shown (numerator).
All Khan Academy content is available for free at www.khanacaemy.org
Understanding 4
Fractions Greater than One
The term improper fractions is used to describe fractions greater than one, such as 
(ten quarters). Representations of a fractions greater than one, with the numerator being greater than the denominator, is frequently used in algebra.
Improper fractions can also be written as mixed numbers. The diagram below shows how(ten quarters) can also be expressed as
(two and two quarters).
We can clearly see that or is equivalent to
The decimal notation for this is 2.5 (two point five).
Understanding 5
Fractions as measures
Fractions are commonly used as measures.
To extend the idea of fractions as numbers, imagine that the following number line is a tape measure used to measure a length of ribbon. The arrow is pointing to two and a quarter metres (
m) of ribbon, which is expressed in decimal fraction notation as one point two five metres (2.25m).
Fractions are often used to measure time, for example:
-
The term half an hour is more commonly used than 30 minutes
-
45 minutes is often expressed as three quarters of an hour
Understanding 6
Fractions as Operators
A fraction acts as an operator when it is applied to a number, set or quantity to find a certain proportion of that number, set or quantity.
Example 1
Find three quarters of twenty four.
There are many ways of solving this. It would be straightforward to find one quarter of 24 (six) and multiply this by three to find three quarters, giving an answer of 18.
Example 2
The original cost of an oven ($1,200) is reduced by. What is of $1,200? What will the discounted price be?
One way to solve this is;
(x 1200) is the same as 1200 ÷ 5, which is 240.
Therefore the discounted price would be $1200 - $240 = $960.
Notice the word of , which is indicative of the operation of multiplication.
Notice also that multiplying by a number which is less than one (e.g.or) results in a smaller number.
Understanding 7
Fractions as Division
Fractions can be used as a representation of division.
Example 1
A quotient such as 3 ÷ 4 can be represented by.
Numbers that can be expressed in this way
Asare known as rational numbers and can be derived from dividing the numerator by the denominator.
Example 2
Three people have to share two choc bars. How much does each person get?
Here is one way to visually represent this problem:
Each person receives one third of each bar, therefore two thirds (
) of a chocolate bar.
Two shared among three can be represented by the division 2 ÷ 3, which is the same as.
Conversely, the symbolcan be referred to as two divided by three.
The quotient of two divided by three is two thirds.
The following video shows how paper-folding strips of paper are used to solve division of whole numbers where the quotients are fractions.
Understanding 8
Fractions as Ratios
Fractions can be interpreted as ratios.
Example 1
In the pictures below there are 5 puppies, 3 females and 2 males.
Part-to-part
The ratio of males to females is 2:3 or
Ther ratio of females to males is 3:2 or
Part-to-whole
The ratio of males to all the puppies is 2:5 or
The ratio of females to all puppies is 3:5 or
When using or interpreting ratios, an important aspect is to be clear about is whether the comparison is Part-to-part or Part-to-whole.
Fractions are used more commonly to represent part:whole ratios.
Example 2: Part-to-part representation
- The instructions for dilution of weed killer state one part weed killer to six parts water.
As a part-to-part relationship, the ratio of weed killer to water is 1:6, and can be demonstrated with a visual model, showing a total of seven equal parts.
- In Timber Town the ratio of children under 18 years to adults is 1:4 (one to four). If there are two hundred people in this town we can say that there are 40 children and 160 adults (the two different parts).
To work this out, we know that there are 5 parts in total and the population (whole) is 200. One part is forty (200 ÷ 5). Four parts (adults) is 4 x 40.
Example 3: Part-to-whole representation
Practice Task 1
1. Starting atwrite a sequence of eight numbers counting by:
a) One half
b) One quarter
c) One tenth
d) One twelfth
2. Find equivalent fractions for:
a)
b)
c)
3. Show how you can calculate:
a)
b)÷
c)
d)+ 
4.Place the following numbers on a number line:
a) 2 
1 
b) 0.5 2.25 0.9 2 1.75 2.8 2.4 0.2 1.5 1
Click here to check your answers.
Practice Task 2
Solve the following problems where fractions are used as operators. There is more than one way to solve each of these problems and thinking about different strategies can be helpful.
- Genni was renovating her laundry. 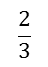of the floor tiles needed to be replaced. The total number of equal sized tiles on the floor was 60. How many tiles had to be replaced?
- How much would you pay for a $132 pair of shoes that have been discounted by 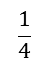of their marked price?
- Which is the larger, 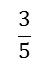of 45 or
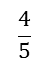of 40?
(We cannot assume that the second one is the largest just because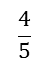is a larger fraction than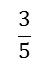, as they relate to different wholes).
Click here to check your answers
Practice Task 3
Draw a visual model to show how six pizzas can be equally shared among eight people if:
- The pizzas are cut into eighths
- The pizzas are cut into quarters
Identify whether the following problems are Part-to-part or Part-to-whole representations and represent the answers using a ratio:
Timber Town has a population of 200 people, 40 of these being children.
a) What is the ratio of children to the town's population?
b) What is the ratio of adults to the town's population?
c) What fraction of the town's population are children?
d) What fraction of the town's population are adults?
On a school excursion, there is one adult supervisor for every group of six children.
a) What is the ratio of supervisors to children?
b) If there are 36 children, how many adult supervisors are required?
c) What fraction of the people on the excursion are supervisors?
Click here to check your answers
Check your Understanding of Fractions
The purpose of this module was to identify how:
- Fractions occur in a wide range of contexts.
- Fractions have many different interpretations.
To demonstrate the following understandings:
- Fractions can be used to describe parts of a whole. eg: 3/4 of the class attended the performance.
- To order, compare, add or subtract fractions, they must relate to the same unit or whole. eg:, we can make the comparison that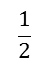a pizza is bigger than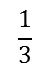of a pizza if both of these fractions are parts of the same pizza (ie the same whole). This would not be the case if we were talking about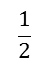of a small pizza and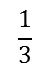of a large pizza.
- Fractions can be used as numbers as placed on the number line
http://syllabus.bos.nsw.edu.au/assets/mathematicsk10/images/s3na043.png - Fractions can be used as measures eg: in the fraction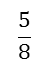you can use the unit fraction
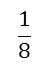and measure to show that it takes 5 of these to make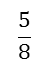 - Fractions can be used as an operator to find a proportion of a number, set or quantity eg: If I have a class of 24 students and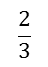of the class went to the swimming pool during the holidays this means that 16 students in my class went to the pool.
- Fractions can be used as a representation of division are a model for division eg: a quotient such as 3 ÷ 4 can be represented by
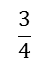
- Fractions can be used to represent a ratio, and this can be of two parts or of a part to a whole. eg: " there are 5 cats to every 7 dogs" could be written as
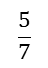. Ratios can be part-part or part-whole. If we consider the ratio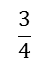a part-part example could be "the ratio of people who own a dog (part) to those who do not own a dog (part)" whereas a part-whole example could be "the ratio of people who own a dog (part) to the people in your suburb (whole).
Does this make sense to you now?
Proceed to the next tab
The system of decimal numbers is an extension of the whole-number number system. Decimal numbers are one way of representing fractions, ratios and percents.
Understanding 1
Decimals
The word 'Decimal' comes from the Latin word decem meaning ten. The decimal system has 10 as its base and is sometimes called a base-10 system. This means that the decimal system is based on "bundles of ten" and using the digits 0,1,2,3,4,5,6,7,8,9 as represented in the diagrams below;
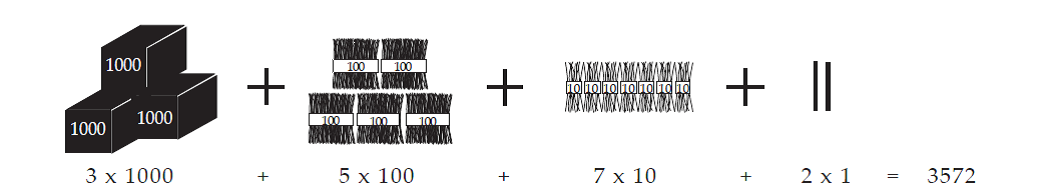
In the decimal system the decimal point separates the ones place from the tenths place. The system of decimal numbers is an extension of the system of whole numbers (see PV Module). Whole numbers are written as digits that correspond to the 'places' ones, ten, hundreds and so on. Positive numbers less than one can be written using the same notation with additional places to the right of the decimal point, such as tenths, hundredths, thousandths and so on.
Decimals are widely used today, especially in areas such as finances, commerce and science. They are also used when measurements require a given accuracy.
Although decimal notation is often used to represent fractions, sometimes fraction notation is more appropriate. For example, it is much simpler to find one third of twenty four (x 24) than to use the decimal equivalent of one third (0.333333 x 24). The threes in this decimal go on indefinitely.
Learning Activity 1
Where do fractions and decimals fit into the base-ten number system?
Watch the following video about the classification of numbers
The video shows how fractions and decimals fit into our number system.
The system of decimal numbers is an extension of the whole number system. (See Place Value module, Big Idea 1, Learning Objects 1.1, 1.2 & 1.3)
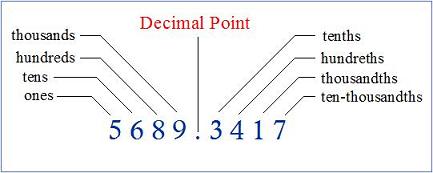
Decimal numbers contain a decimal point, which identifies where the ones place is located, that is, immediately to its left.
The decimal point also signifies the values of the digits to its right, being tenths, hundredths, thousandths and so on.
The position of a digit in a number determines its value.
345.1258
In the above number…
The 3 is in the hundreds place, so the value of the 3 is 300 (3 x 100)
The 4 is in the tens place, so the value of the 4 is 40 (4 x 10)
The 5 is in the ones place, so its value is 5 (5 x 1)
The 1 is in the tenths place, so the value of the 1 is 1 tenth or 0.1 (1 x
)
The 2 is in the hundredths place, so it represents 2 hundredths or 0.02 (2 x 
)
The 5 is in the thousandths place, so it represents 5 thousandths or 0.005 (5 x 
)
The 8 is in the ten thousandths place, so it represents 8 ten thousandths or 0.0008 (8 x
)
Any number can be renamed in terms of its place value parts.
(See Place Value module, Big Idea 1, Learning Objects 1.1, 1.2 & 1.3)
Below are some examples of how a number, in this case 345.1258, can be written in expanded notation.
345.1258 = 3 hundreds + 4 tens + 5 ones + 1 tenth + 2 hundredths + 5 thousandths + 8 ten thousandths
or
345.1258 = 300 + 40 + 5 + 0.1 + 0.02 + 0.005 + 0.0008
or
345.1258 = 34 tens + 5 ones+ 1 tenth + 25 thousandths + 8 ten thousandths
As the video has shown, all whole numbers and fractions are rational numbers, which can be written as exact decimals.
Example
The fraction three quarterscan be written as a decimal. Three quartersis equivalent to seventy five one hundredths,
, and therefore can be written as the decimal zero point seven five (0.75).
The next module/big idea will demonstrate how this is equivalent to seventy five percent (75%).
Here are further examples:
| Rational Number | Expressed as a Fraction | Expressed as a Decimal |
|---|---|---|
| three fifths | | 0.6 |
| nineteen | | 19.0 |
| five and two tenths | | 5.2 |
| two thirds | | |
| one eighth | | 0.125 |
Learning Activity 2
Pi, π, An irrational number
An interesting example of an irrational number is Pi (Ï€). It cannot be expressed as a fraction a/b where a and b are whole numbers (see module 1).
The value of pi = Ï€ is 3.14159… This decimal value goes on forever. This decimal number goes on for ever with no repeating pattern.
The following link shows Pi to one million decimal places!
http://www.piday.org/million/
The YouTube video below is a fun and interesting way to think about the kind of number that Pi is.
Common Misconceptions about Decimals
1. Longer is larger
A common misunderstanding when comparing numbers originates from the separation of decimal numbers into two whole numbers; that is, the sets of numbers on each side of the decimal point are treated as whole numbers.
The following examples show how this misunderstanding can go unrecognised because sometimes it results in a 'fluke' correct answer:
| Which is smaller? | Incorrect reasoning | Correct reasoning | Correct answer |
|---|---|---|---|
| 5.17 or 5.6 | 5.6 is smaller, because 6 is less than 17 | 5.17 is smaller because it has one tenth while 5.6 has six tenths. The seven hundredths are not relevant as they are smaller than tenths | 5.6 |
| 6.42 or 6.801 | 6.42 is smaller, as 42 is less than 801 | 6.42 is smaller because it has four tenths while 6.801 has eight tenths | 6.42 |
| 14.5 or 14.50 | 14.5 is smaller as 5 is smaller than 50. | They are both have the same value because 5 tenths is the same as 50 hundredths | Both the same |
2. Shorter is larger
This is another common misunderstanding when comparing numbers. It occurs when the decimals are incorrectly seen as fraction denominators: the larger the denominator, the smaller the fraction.
The following examples show how this misunderstanding can go unrecognised, as sometimes it results in a 'fluke' correct answer:
| Which is smaller? | Incorrect reasoning | Correct reasoning | Correct answer |
|---|---|---|---|
| 7.12 or 7.6 | 7.12 is smaller, as twelfths are smaller than sixths | 7.12 is smaller as it has one tenth whereas 7.6 has six tenths | 7.12 |
| 6.4 or 6.8 | 6.8 is smaller, as eighths are smaller than fourths/quarters | 6.4 is smaller as it has four tenths whereas 6.8 has eight tenths | 6.4 |
| 15.3 or 15.30 | 15.30 is smaller as thirtieths are smaller than thirds | They are both have the same value as 3 tenths is the same as 30 hundredths | Both the same |
Write each of the following numbers as fractions and decimals.
Sample answers have been given for the first number.
| Number | Fraction | Expressed as a Decimal |
|---|---|---|
| One quarter |  | 0.25, 0.250 ... |
| One eighth | ||
| Three eighths | ||
| One tenth | ||
| One fifth | ||
| Three fifths | ||
| One third | ||
| Two and six tenths | ||
| Twelve and three quarters | ||
| Fifty and a half |
Click here to check your answers
Practice Task 2
Write each of the following numbers in expanded notation, renaming in terms of the place value parts:
a) 25.6
b) 160.375
c) 3 451.4672
Click here to check your answer
Check your Understanding of Decimals
The purpose of this module was to identify how:
- fractions and decimals fit into our number system.
- the system of decimal numbers is an extension of the whole number system.
To demonstrate the following understandings:
- Each digit in a number has a place value depending on its position or place.
- Numbers can be partitioned and named renamed in terms of the position of each digit.
- The decimal point separates the whole number places from the decimal number places.
Does this make sense to you now?
Please continue on to the next tab
Fractions, decimals and percentages are related and can be used to express the same number, or proportion in different ways.
Understanding 1
Relating Decimals, Fractions and Percents
The learning activities in the previous two modules focussed on numbers represented as fractions , decimals and ratios. This module focuses on percents, another way of representing rational numbers.
Any rational number, whether a fraction or a whole number, can be written as a fraction, decimal or percent.
The term percent is simply another name for hundredths and as such percents are rational numbers with a denominator of 100. For example, 25% (twenty five per cent) is the same as
(twenty five hundredths). 25% orcan also be written in decimal notation as 0.25 (zero point two five).
By the end of this module you should be able to fill in a chart similar to this one.
| Number | Fraction | Decimal | Percent |
|---|---|---|---|
| five | | 5.0 | 500% |
| two and one eighth | | 2.125 | 212.5% |
| three quarters | | 0.75 | 75% |
Learning Activity 1
Relating Decimals, Fractions and Percent
Please go to the link below and complete the activities suggested below.
Math Is Fun Virtual Manipulative
Activities to demonstrate the relationship between fractions, decimals and percents, and reinforce and extend your understandings of percents being another way to represent fractions:
1. Place your curser on the pizza at the 3 o'clock position, or 90 degrees. At this position one whole pizza is shown, the 100 grid is fully shaded (100 percent or 100%) and the number one is identified on the zero to one number line.
(one whole) = 100% (one hundred out of one hundred equal parts) = 1
2. By rotating the curser in an anti-clockwise direction around the pizza, shading the grid or moving along the number line, you can select a portion of the pizza.
Shade one of the 100 squares on the grid. This is one out of 100 equal parts, therefore, 1% (per cent) of the grid. Notice that one hundredth of the pizza appears, and the pointer is a very small distance past zero on the number line.
Imagine the number line from zero to 1 divided into one hundred equal parts. One of these parts is one hundredth, or 0.01. This part is also one tenth of a tenth, or one tenth of 0.1.
(one one-hundredth) = 1% = 0.01 (zero point zero one)
3. Highlight the top row of the grid, that is, ten of the one hundred squares. You have highlighted one tenth of the square, and will notice that one out of ten equal parts of the pizza has appeared. The pointer shows one tenth, or 0.1 (zero point one) on the number line. This can also be written as 0.10, showing that one tenth is exactly the same as ten hundredths. and 10/100 are equivalent fractions (add link – FDRP LO1).
(one tenth) = 10% = 0.1 (zero point one)
4. Move your curser to show:
(one half) = 50% = 0.5 (zero point five) or 0.50
(one quarter) = 25% = 0.25 (zero point two five)
(seven hundredths) = 7% = 0.07 (zero point zero seven)
(three quarters) = 75% = 0.75 (zero point seven five)
(seven hundredths) = 7% = 0.07 (zero point zero seven)
(nine tenths) = 90% = 0.9 (zero point nine) or 0.90
(ninety nine hundredths) = 99% = 0.99 (zero point nine nine)
Understanding 2
Representing Decimals to Thousandths
A one thousand grid can be used to represent one whole (1), and to demonstrate decimals up to thousandths.
The entire grid represents one (1), or one whole.
The grid can be divided into 10 equal parts, or tenths. One of these ten equal parts, or one tenth of the grid (), is shaded in red.
One tenth, the red portion, can be divided into ten equal parts (the yellow section shows this). The yellow portion is a one hundredth () as 100 of these make the whole.
A one hundredth (), the yellow portion, can also be divided into ten equal parts (the blue section shows this). The blue portion is represents one thousandths () of the whole, as 1000 of these thousands makes the whole.
The following statements can be made:
-
The red area is one tenth (
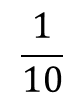) or zero point one (0.1) of the whole grid -
The yellow area is one hundredth (
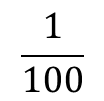) or zero point zero one (0.01) of the whole grid -
The blue area is one thousandth (
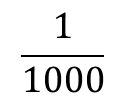) or zero point zero zero one (0.001) of the whole grid -
10 tenths equal one whole (
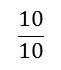= 1) -
100 hundred hundredths equals one whole (
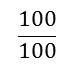= 1) -
1000 thousandths equals one whole (
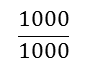= 1) -
10 hundredths (yellows) equal one tenth (red)
-
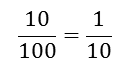; 0.10 = 0.1 -
10 thousandths (blues) equal one hundredth (yellow)
-
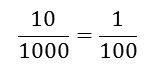; 0.010 = 0.01 -
100 thousandths (blues) = one tenth(red)
-
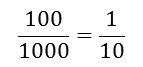; 0.100 = 0.1 -
The shaded area of the grid is one hundred and eleven thousands (
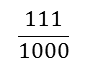) of the grid, which can also be expressed as the decimal fraction zero point one one one (0.111) -
In expanded form or expanded notation this is:
One tenth + one hundredth + one thousandth
(
) or (0.1 + 0.01 + 0.001) or (
) or (
)
Learning Activity 2
One Thousand Grid: A visual model for decimal fractions
The following video uses a thousandths grid in a similar way, to demonstrate writing decimal fractions:
The second example in the video focuses on the shaded area being 500 one thousandths of a whole 1000 (comprising one thousandths). It is written as
or 0.500.
It is easy to see that this shaded area is one half of the whole grid.
This shaded area can also be broken up into 50 hundredths. The fraction 50 hundredths (
) is equivalent to 500 thousandths ().
Furthermore, the shaded area in the video can be broken up into five tenths. The fraction five tenths (
) is equivalent to the fraction 50 hundredths () and 500 thousandths ().
All of these fractions have the same value of one half (), and so they are equivalent fractions.
Decimal notation
0.5 = 0.50 = 0.500
The decimal notation does not require the zeros after the five. Unlike whole numbers, a zero on the end (right hand side) does not change the value of the decimal. However, the zeros can sometimes assist when adding and subtracting decimals.
Learning Activity 3
Fractions Greater than One
Click on the following link from Illuminations Resources for Teaching Math:
FRACTION MODELS
Follow these instructions:
- Select the tab 'wide range' at the top of the display screen. This sets the numerator range at the bottom of the screen as 0 – 100, and the denominator range at 1 – 25. The fractions will therefore be improper, or greater than 1, because the numerator will be greater than the denominator.
- Select the 'area' model option, located on the right hand side under the table. Use the plus and minus tabs either side of the numerator and denominator settings to select a numerator of 5 and a denominator of 3. You will see five thirds represented on the area model on the screen. Above this you will see how this number is expressed as a fraction (or improper fraction)
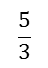, a mixed number (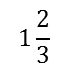) , a decimal (1.6667), and a percent (166.67%). Note that the decimal and percent have been rounded up; otherwise they would go on forever.
Look at the different models (length, area, region, set). - Try other numbers greater than one, looking at the different visual representations. Note how they are expressed in improper fractions, mixed numbers, decimals and percents.
Understanding 3
Relating Decimals, Fractions and Percent using a Number Line
The number line below is marked in increments of one hundredths from zero to 0.36. Notice where the following decimal numbers, all containing similar digits but in different places, are placed on the number line:
| 0.257 | 0.05 | 0.023 | 0.307 | 0.175 | 0.12 |
|---|
The decimal 0.023 has a zero in the tenths place, so it is less than one tenth (0.1). It decimal 0.023 has two hundredths. It also has 3 thousandths, so it is just past the 2 hundredths mark (three tenths past the mark).
The decimal 0.05 has a zero in the tenths place, so it is less than one tenth (0.1). is bigger than 0.023, as it has more hundredths.
The decimal is 0.12 has 1 tenth and 2 hundredths, so is two hundredths past the one tenth (0.1) mark.
The decimal 0.175 is also between 0.1 and 0.2, but it is closer to 0.2 because it has seven tenths. It is half way between the seven and eight tenths marks because it also has 5 thousandths.
The decimal 0.257 is between 0.2 and 0.3. It has five hundredths, so it is about half way between 0.2 and 0.3. It also has 7 thousandths, so it is just past half way between 0.2 and 0.3.
The decimal 0.302 is only 2 thousandths more than 0.3, so it is only slightly past the 0.3 mark.
This time the three different representations of rational numbers, fractions, decimals and percents, have been placed on a blank number line.
| 15% | 0.28 | | 70% | 0.115 | 1 | | | 0.3 |
|---|
| 15% | 0.28 | | 70% | 0.115 | 1 | | | 0.3 |
| | | | | | | | | |
* 
and
are close approximations. The decimal 0.115 is actuallyand 5 thousandths and is a little more than, because it is 0.3333333.
Examples of how percentages are used in real life
Example 1
There is a sale on homewares at a department store with 25% of selected items. A dinner set before the sale cost $130.
What will it cost you now?Solution: We recognise that 25% is equal to. We can then work outof $130 which is $32.50.
(we know this because half of 130 is 65 and half of 65 is 32.5. This is the same as dividing 130 by 4).
Therefore you can purchase the dinner set for $130 - $32.5 = $97.50
Example 2
A property that was on the market for $450,000 last year has decreased in value by 10%. How much will you save by buying it now?Solution: We recognise that 10% is the same as. Nowof $450,000 is $45,000. Therefore you would save $45,000 by buying the property now.
(Note that a 10% discount off a small item such as a $20 t-shirt amounts to just a few dollars, in this case $2. Whereas a 10% discount of a $450,000 property is a very worthwhile $45,000. So the significance of what a 10% discount might mean to us depends on the whole we started with).
Common Misconceptions for Decimals and Fractions
Decimals stop at hundredths - NO
Examples of decimals beyond hundredths:
A millimetre (mm) is one thousandth of a metre
1mm = 0.001m
2.44 micrograms is equal to 0.00244 milligrams.
Common Misconceptions for Ordering Fractions
1. The larger the denominator, the bigger the fraction
This is true for unit fractions (fractions with a numerator of one). There is an inverse relationship between the number of parts and the size of each part: The larger the number of parts (the denominator), the smaller the size of each part (the numerator). Unless the problem context indicates that two fractions relate to different wholes, we assume both relate to the same whole. With this in mind, it makes sense that the more parts into which the whole is divided, the smaller they will be.
Example: Compare one eighthto one fifth
If we are referring to the same whole, such as a portion of a cake (modelled below), we can see that the more parts into which it is divided, the smaller each part will be.
In the visual representation, we can clearly see thatis larger than.
Five people sharing above cake, soeach
Eight people sharing same sized cake, soeach.
When we are comparing just one of each part, such as one eighthto one fifth (), the bigger the denominator, the smaller each part will be.
The numerator is one (
)
When one or both fractions are not unit fractions:
This time, we will compare one fifth(), and three eighths (
). We know that eighths are smaller than fifths, but we must note that this time there are three eighths, not just one.
In the diagram below, we can see thatis a bigger portion than.
Person A ate one fifth () of the cake.
Person B ate three eighths () of the cake.
If we cannot reliably compare the fractions with different denominators visually, as in the diagram above, we need to change one or both of the fractions into equivalent fractions for a common denominator.
It is easy to recognise that four fifths () is greater than two fifths (), because each of the parts (fifths) is the same size. Four is greater than two, somust be greater than .
What about comparing four fifths () and seven tenths (
), which have different denominators?
As was seen on the fraction wall, each fifth is equivalent to two tenths. This is demonstrated in the model below:
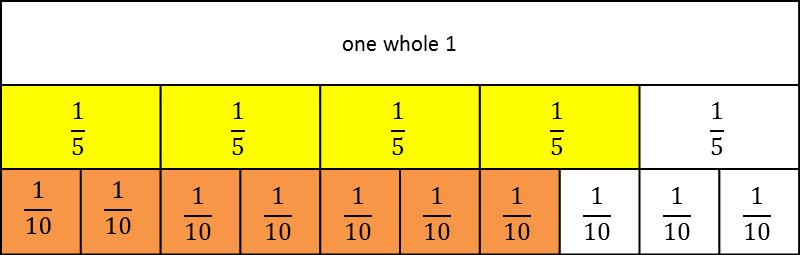
Changing four fifths () to the equivalent fraction eight tenths (
) makes it much easier to see that four fifths () is greater than seven tenths ().
Practice Task 1
1) Complete the table so that the numbers in each row represented by fractions, decimals and percents are equivalent:
| Fraction | Decimal | Percent |
|---|---|---|
| | 1.1 | 110% |
| | ||
| 0.04 | ||
| 25% | ||
| | ||
| 350% | ||
| 0.125 |
2) Order the following numbers from smallest to largest:
0.125
1.5
1.45
0.25
0.81
0.09
1.1065
3) Write at least four equivalent fractions for each of the following fractions:
Click here to check your answers
Practice Task 2
1) Relating decimals, fractions and percent using a number line
Click on the link below and complete the activity by placing all of the fractions, decimals and percents on the number lines from ICTgames.
Equivalence of Fractions, Decimals and Percents
2) Place the following fractions, decimals and percents on a single number line:
10%
0.375
50%
1.3
128%
0.002
3) Take a look in the day's newspaper and highlight every time percentages are referred to or used. This is an activity that students could do as well.
Click here to check your answers
Check your understanding of the relationship between fractions, decimal and percent
The purpose of this topic was to demonstrate the following understandings;
- A number can be represented as a fraction or a decimal.
- A percent is a fraction out of one hundred and are a very commonly used in everyday life. Percents can also be understood as hundredths
Does this make sense to you now?
Please proceed to the next tab
An understanding of percent relationships helps us to compare and represent increasing and decreasing proportions.
Understanding 1
Proportional Reasoning
Using percent in to solve everyday problems requires proportional reasoning. Proportion reasoning involves the consideration of number in relative terms,rather than absolute terms.
For example, converting a fraction of
(five sixths) to a percent is equivalent to finding what part of 100 is equal to five parts out of six.
In numerical notation this can be expressed as
One way to convert a fraction into a percent is to remember that any fraction can be interpreted as a quotient (division) (see FDRP BI2 Fractions as division). In the case of, this is 5 ÷ 6. Using a calculator, 5 ÷ 6 is
. Remembering that percents are hundredths, this can be expressed as
.
Knowing this can make understanding of everyday maths language easier, such as in the following example of percent decrease.
Understanding 2
Percent Decrease and Increase
Example 1
Mathematical language and data presented in media is not always clear. Being able to understand percent use and its relationship with fractions, decimals and proportional reasoning helps us to more easily interpret information about our world.
So do you think that an increase in the number of deaths by drowning from 57 to 64 the following year is an alarming increase?
Click on the following link to read the news story "Drink swim deaths rise"
http://www.mercurynie.com.au/mathguys/mercury.htm
Click on data representation and then on the article ""Drink swim deaths rise"
The second paragraph refers to percent increase:
Alarming figures show a 12.3 per cent increase in drowning deaths in the 25 to 34 year old age group, and 90 per cent of the deaths were male.
The 12.3% increase in drowning in the 25 – 34 age group is referred to as 'alarming' by the reporter, but for a clearer perspective we would have to know the actual numbers.
The graph in the article shows the number of drowning for each age group, which totals 292, as mentioned in the article. The number of drowning in the 25 – 34 age group is the highest on the graph, and appears to be about 64 in number. This number of 64 includes the 12.3% increase, so the 64 is comprised of the previous year's 100% plus the 12.3% increase. Therefore the number 64 represents 112.3% of the previous year's number of deaths by drowning in the 25 -34 age group.
To work out 1% of 64, we can divide 64 by 112.3 to get 0.5699. We can therefore workout that in the previous year 57 people (100 x 0.5699) drowned and that in the following year 57 + 7 more (12.3 x 0.5699) people drowned. Note that in a context like this in which the numbers calculated are numbers of people, rounding to the nearest whole number is appropriate.
Example 2
Take a look at the money cards above and consider the following:
-
An increase from $100 to $200 is an increase of 100%
-
Whereas a decrease from $200 back to $100 is a decrease of 50%
-
An increase from $100 to $150 is an increase of 50%
-
Whereas a decrease from $150 back to $100 is a decrease of 33
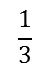% (33.83 ̇%) -
An increase from $160 to $200 is an increase of 25% (because $40 is 0.25 of $160). Note that 0.25 is
-
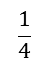
Whereas a decrease from $200 back to $160 is a decrease of 20% (because $40 is 0.2 of $200). Note that 0.2 is
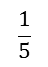
Example 3
A few years ago, a Tasmanian politician was up in arms about the drop in poker machine profit tax from 6% to 1%. He said that the taxed had dropped by 500%.
A solid understanding of percent would help recognise that because 100% is the whole, any decrease of more than 100% would not make sense as it would result in a negative. In other words, If the drop was 100%, the tax would be zero.
It is important to consider that a change in percent is always considered in relation to the original amount. The tax dropped from 6% (the original whole amount of tax) to 1%, so it dropped by five out of six. From our previous calculation, we know thatis .
We can see that the actualdecrease is a considerable drop in tax.
Understanding 3
Using Percent to Compare Numbers
http://www.mercurynie.com.au/mathguys/mercury.htm
The 1996 news story "Drink swim deaths rise" also contains an example of use of percent to make comparisons. Look at the same paragraph as the previous section:
Alarming figures show a 12.3 per cent increase in drowning deaths in the 25 to 34 year old age group, and 90 per cent of the deaths were male.
As well as the mention of a 12.3% increase, percent is used to highlight the number of male deaths compared to female deaths.
In the previous section we calculated the number of deaths for two consecutive years, being 57 and 64. Using knowledge of percent or fractions (in this case hundredths) as an operator (see FDRP BI2 Fractions as operators), we can work out the numbers of males and females for a clearer understanding of the data. Again, in this context where the numbers calculated are numbers of people, rounding to the nearest whole number is appropriate.
| Total Number of Males and Females | Approximate Number of Males | Approximate Number of Females | |
|---|---|---|---|
| Year A | 57 | 51 0.9 (90%) x 57 = 51 | 6 0.1 (10%) x 57 = 6 |
| Year B | 64 | 58 0.9 (90%) x 64 = 58 | 6 0.1 (10%) x 64 = 6 |
The actual numbers of male and females who drowned, rather than using percents, may send a clearer message than percents about the difference between male and female drownings.
Understanding 4
Using Percentages in Simple Interest Calculations
When money is borrowed or invested for a fixed time at a fixed interest rate and the interest rate is calculated only on the initial investment, simple interest (sometimes known as flat interest) is calculated. (Note: that simple interest is not the only way that interest can be calculated).
The following formula is useful for calculating simple interest:
I = P x R x T
where; I = Amount of interest,P= Principal (Amount invested or borrowed),R= Interest rate per annum (per year) as a decimal eg: 5%=0.05 andT= Time of investment in years
(Note also that in an algebraic formula like this we do not need to put in the multiplication symbol. We can just write I =P R T)
You may have also seen this formula written like this:
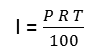
In this case you would enter the rate as a fraction.
For example if the interest rate was 5% you would enter a 5 in place of the r so you would have 
( note that the 
part is already in the formula)
Either form can be used, it is your own personal preference.
Please refer to Examples 4 and 5 below for some worked examples of simple interest calculations
Example 1
Your weekly pay of $748 will increase by 3.5%. What will your new weekly pay be?
Sample solving strategy:
| Step 1. Find 1% x 748. 1% = | x 748 = 7.48 (748 ÷ 100) |
| Step 2. The pay rise is 3.5% which is half of 7%. Multiplying by 7 and halving the product is a helpful mental strategy if no calculator is available. | ( 7 x 7.48 = 52.36 |
| Step 3. Add the pay increase to the original whole. | $748 + $26.18 = $774.18 |
)
If a calculator is available, use the fraction as an operator method:
x 748 = 0.035 x 748
0.035 x 748 = 26.18
748 + 26.18 = $774.18
Example 2
The average price of bread increased from $2.80 to $3.70 over three years? What was the percent increase?
Sample solving strategy:
The price increase was $3.70 - $2.80 = 90c
Therefore the price increase is 0.9 out of the original 2.80
0.9 ÷ 2.8 = 0.32
0.32 = 32% price increase
Example 3
You need to borrow $5,000. What is the best two-year deal, A or B?
| Deal A Pay back with 12.5% interest within two years. | Deal B Pay back half ($2 500) interest free within 6 months, then the rest at 30% interest. |
| Deal A sample solution strategy: 12.5% is half of 25% Pay back $5 000 + $625 = $5 625 | Deal B sample solution strategy: Pay back $2 500 + $2 500 + $750 Pay back $5 750 |
So deal A is the best deal.
Example 4
$4200 is invested at 5.2% pa. flat for 18 months
How much interest does it earn?
What is the total amount returned to the investor?
Solution
P = 4200
R = 5.2% = 0.052
T = 18 months = 1.5 years
So since I = PRT
I = 4200 X 0.052 X 1.5
I = 327.6
Therefore the interest earned is $327.60
Total in the account = 4200 + 327.6 = $4527.60
Example 5
Find the interest charged if a loan of $7000 is made for three and a half years at 12% flat.
Solution
P = 7000
R = 12% = 0.12
T = 3.5 Years
So since I = P R T
I = 7000 x 0.12 x 3.5
Therefore I = $ 2940
Practice task 1
You want to buy two T-shirts. Which is the best buy, Shop A or Shop B?
| Shop A. Buy two Bonds Tees at $25 each and get 30% off the second T-shirt. | Shop B. All Bonds Tees 25% off normal price of $30 each. |
Click here to check your answer
Practice Task 2
A survey of 1000 females showed that the number of smokers increased by 8% over two years. In the original survey, the number of smokers was 238. What was the number of smokers after 2 years?
Click here to check your answer
Practice Task 3
The staff of a company decreased from 55 to 25. What was the percent decrease?
Click here to check your answer
Practice Task 4
John paid $14 000 for his car. This price included 15% sales tax. What was the actual price of the car before sales tax?
Click here to check your answer
Practice Task 5
Find the interest charged if a loan of $ 9500 is made for 2years at 11.5% flat.
Click here to check your answer
Check your Understanding of Percent
The previous module showed how percents are hundredths and as such are another way of representing rational numbers. However, learning with relation to percent cannot be limited to this understanding, but must also be linked with proportional reasoning as well as decimals and fractions.
Percents are frequently used in real life situations such as when working with interest rates, discounts and price changes. Percents are also often used to compare two quantities.
The purpose of this module was to further develop your knowledge of the meaning of percent by exploring how percents can be used in real life contexts.
- Percentages can be used to show percent increase or decrease.
- Percentages can be used to compare numbers.
- Percentages are used in interest calculations
If you have completed all the lessons and activities and feel you have a good understanding of each topic, then test yourself with the module Quiz for the Fractions, Decimals, Ratios and Percentages modules
Good Luck!!
Module 2: Fractions, Decimals, Ratios and Percentages Quiz
Click on the link below to take the online self-assessed quiz.
There are 10 mathematics questions on the Quiz and they are about the information in this module.
To pass this quiz, you will need to get a mark of 80%. Feedback will be provided for both correct and incorrect answers at the end of the Quiz. If you answer questions incorrectly, then it is strongly recommended that you review the sections of the modules to review those topics. You will be able to re-take the quiz if needed.
Make sure to enter your name and email address in the quiz so your results can be mailed to you for your records. You may need to show your results to your university.
Module 2: Fractions, Decimals, Ratios and Percentages Quiz
Holt Mathematics Lesson 6-1 Relating Decimals Fractions And Percents Answers
Source: https://www.utas.edu.au/mathematics-pathways/pathways-to-health-science/module-2-fractions-decimals-ratios-and-percentages
Posted by: ruizwarsted.blogspot.com
0 Response to "Holt Mathematics Lesson 6-1 Relating Decimals Fractions And Percents Answers"
Post a Comment